前言

推荐选这课，老师（蒋老师）说平时不用去（也没有任何签到）。

课程大作业是随便选一个关于网络科学的论文讲一下，实测很水。

虽然这课在课表上占了3大节课，但是其实每次最少讲15分钟，最多讲1小时就下课了。

而且下面我写的都是划的重点，非常清晰，背会就行。

期末是闭卷考试！

第一节课

不考

第二节课

网络是真实世界中的，图是网络的数学表达。

求图最短路径（BFS/Dijkstra）

使用BFS

由于该图为无权图，采用 BFS 算法求最短路径。
从起点 s 出发，将 s 入队并将其距离设为 0。
每次从队列中取出一个节点 u，访问其所有未被访问的邻接节点 v，
将 v 的距离设为 dist[v] = dist[u] + 1，并记录其前驱为 u。
因为 BFS 按层遍历，节点第一次被访问时即得到了最短路径。
当终点 t 被访问时，其距离 dist[t] 即为最短路径长度，
通过前驱数组可还原最短路径。

图中的其他概念

直径（Diameter）：The longest shortest path in a graph.

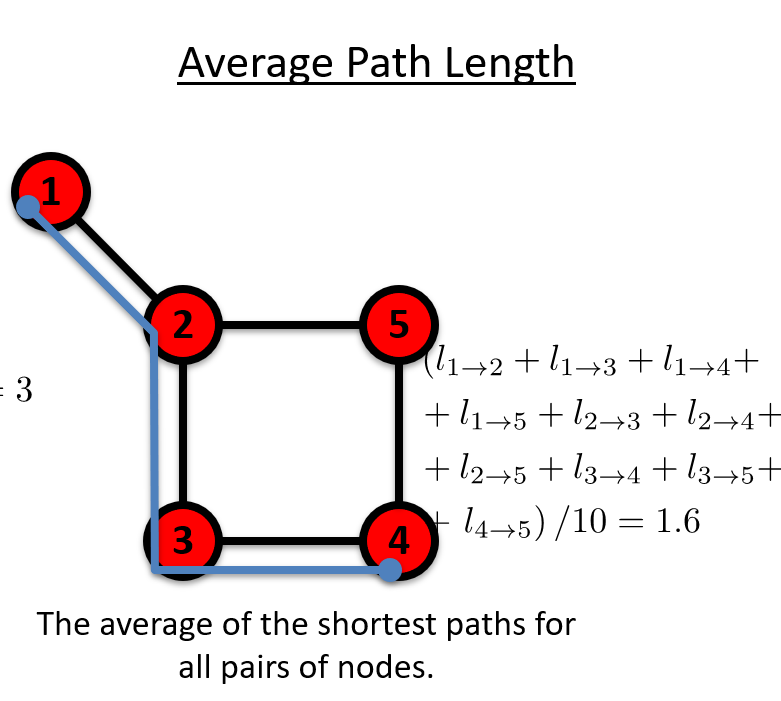
平均路径长度（Average Path Length）：The average of the shortest paths for all pairs of nodes.

环（Cycle）：A path with the same start and end node.

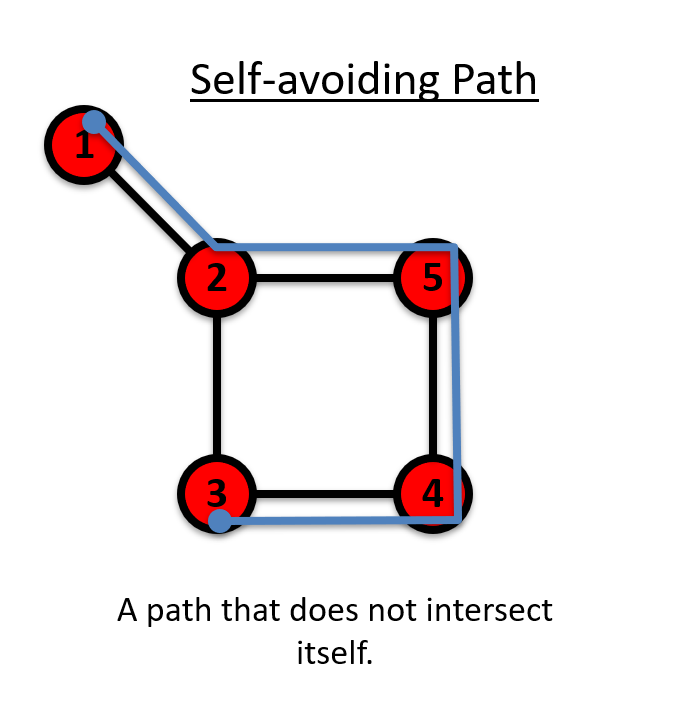
自避路径（Self-avoiding Path）：A path that does not intersect itself.

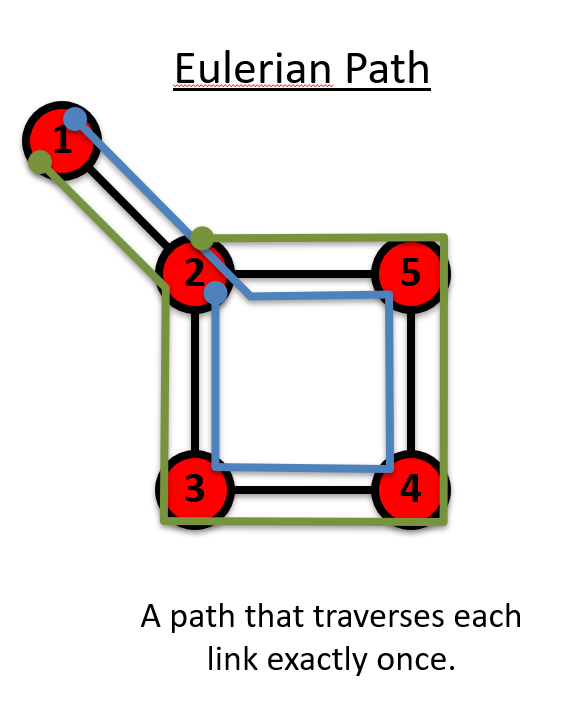
欧拉路径（Eulerian Path）： 在图中不重复经过边的一条路径。

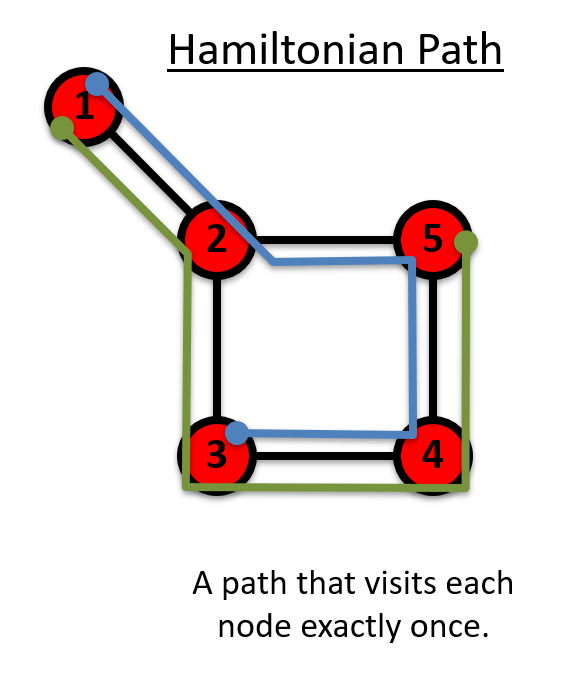
哈密顿路径（Hamiltonian Path）：A path that visits each node exactly once.

无向图的连通性

连通图 / 非连通图； 连通分量；桥

👉 连通图：
在无向图中，任意两个顶点之间都存在一条路径。

👉 非连通图：
由 两个或以上连通分量 组成。

👉 桥（割边）定义：

删掉这条边后，图会变成非连通图

📌 连通分量 =

一个“内部连通、与外部不连通”的最大子图

孤立部分：不属于最大连通分量的其余连通分量

总结：一个无向图如果任意两点之间都有路径，则是连通的；
删除一条桥会使图变为非连通图，从而分裂成多个连通分量，其中最大的称为 Giant Component，其余为 Isolates。

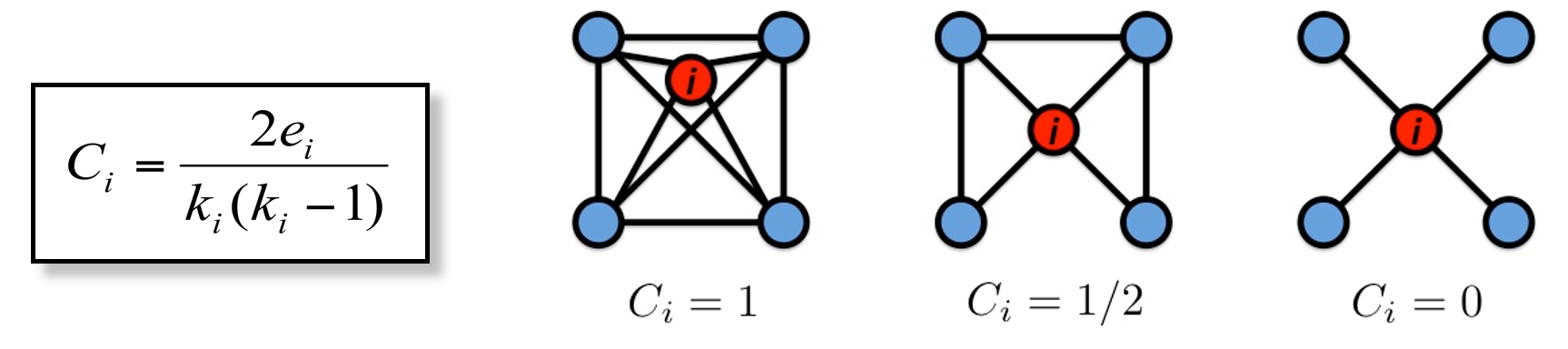
聚类系数

重点：给你一个节点，你要会算这个节点的聚类系数。

聚类系数呈现的是某个节点的邻居相连的程度，记作Ci，i就是当前节点

ki 是节点i的邻居个数（也就是节点i的度数）。

Ci = 邻居的度/邻居理论上最大的度

邻居理论上最大的度 = ki(ki-1)/2 ，也就是C(ki, 2)，邻居的度就是所有邻居之间的边数。

全局聚类系数

与聚类系数不同，全局聚类系数 ≠ 平均聚类系数。

全局聚类系数更偏向整体结构，计算方案是：

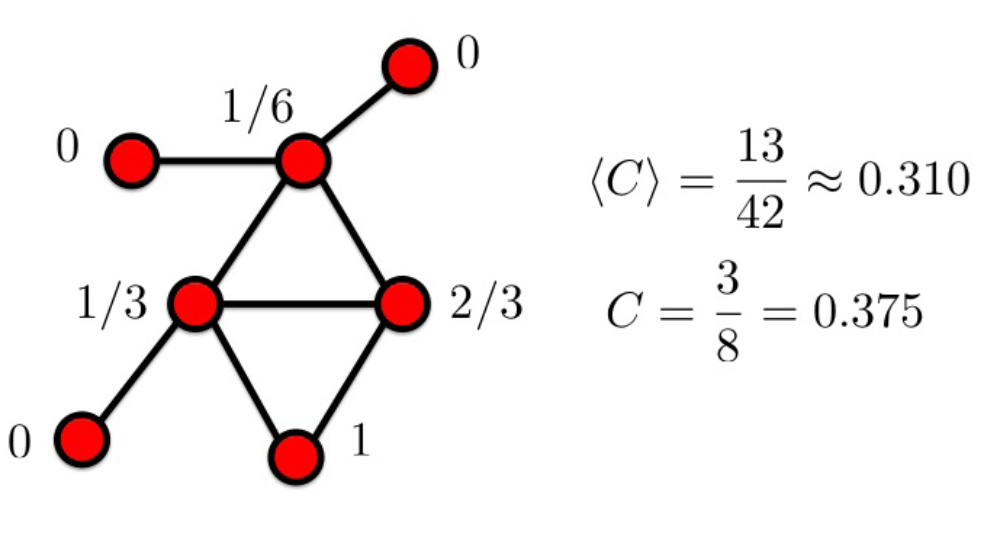
C=网络中闭合三元组个数/网络中所有连通三元组个数=3*三角形个数/连通三元组个数，

连通三元组个数=ΣC(第i个节点度数, 2)，比如下面的图，三角形有两个，所以分子是6，

然后度数小于等于1的节点对三元组贡献是0，度数=2的贡献为1，度数=3的贡献为3，

度数为4的贡献为6，所以一共有16个三元组，所以是3/8。

平均聚类系数＝Σ局部聚类系数/节点总数

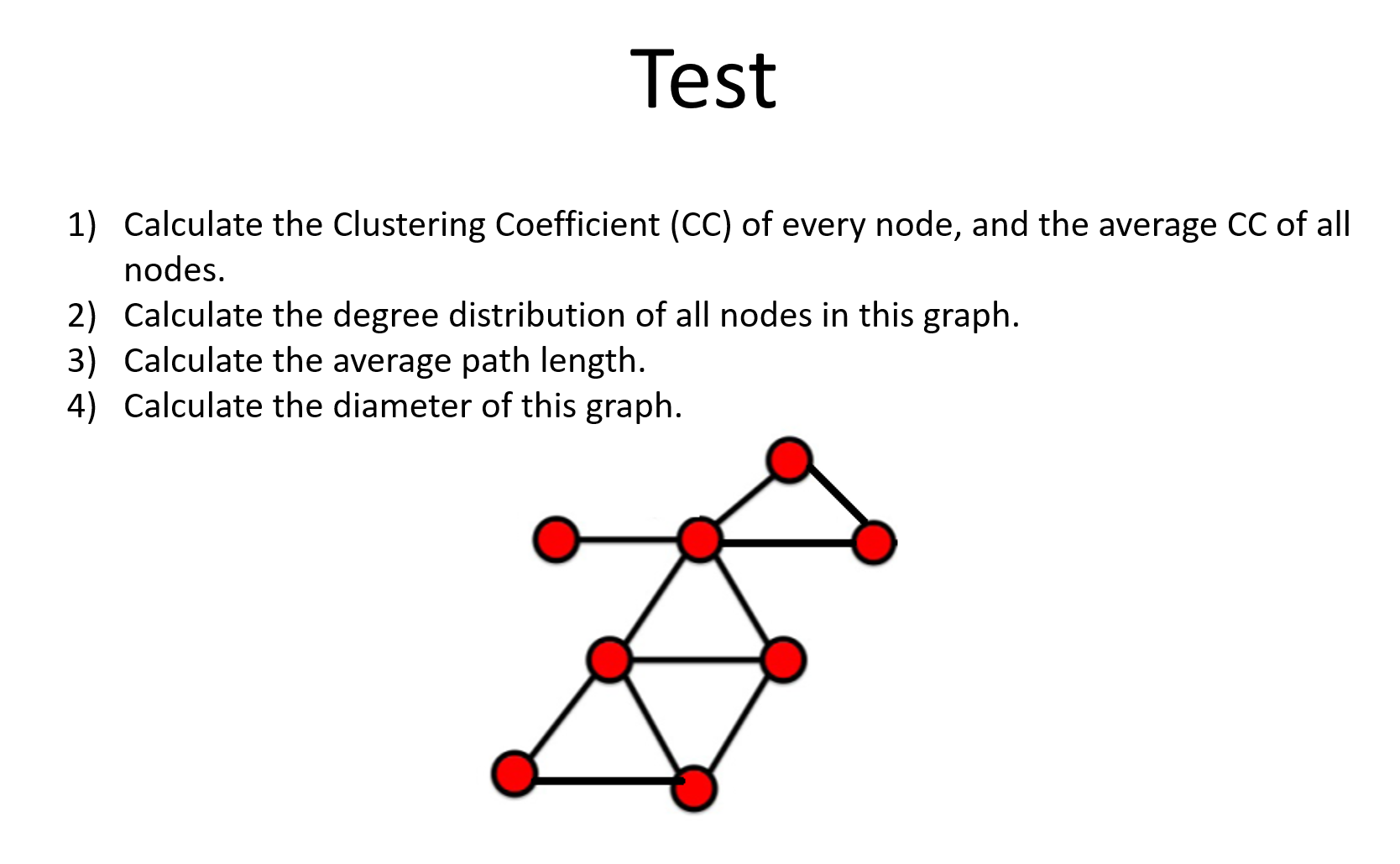
1) 计算每一节点的聚类系数，和平均聚类系数。

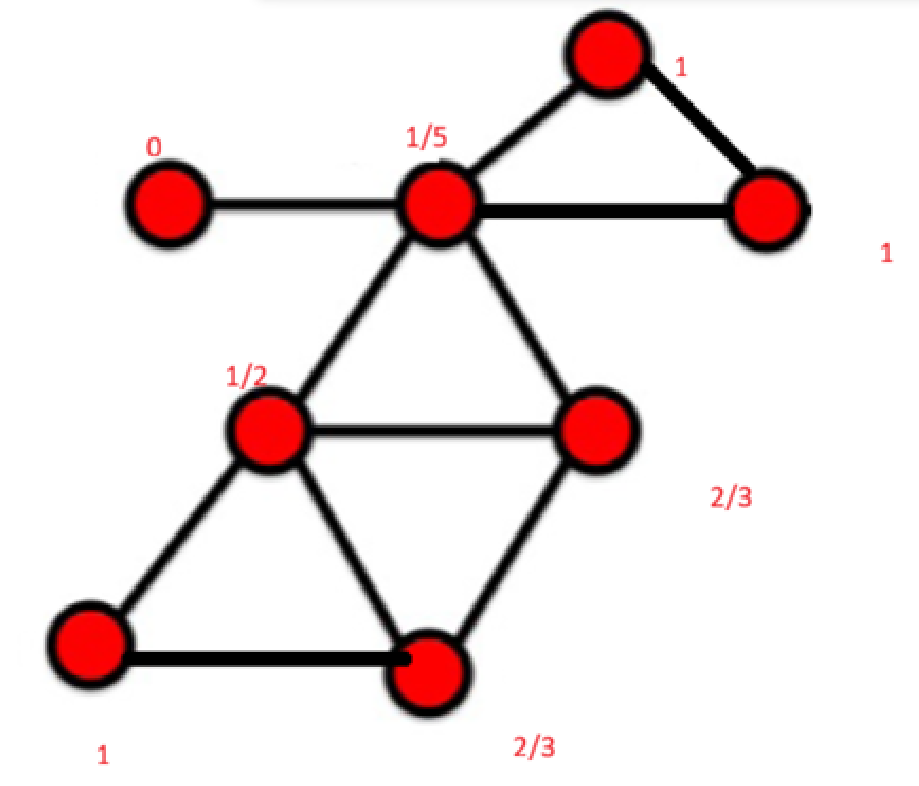
Avg=0.629。

2）P(0) = 0, P(1) = 1/8, P(2) = 3/8, P(3) = 2/8, P(4) = 1/8, P(5) = 1/8。

3）全图一共有C(8, 2) = 28对点，长度总共51，所以AvgPathLength = 28/51。

4）全图最大最短路径是3，所以直径 = 3。

第三节课

考点：随机网络的概念是什么？它是怎么定义的？ER模型怎么生成（过程是怎么样的）？G(N,p)是重点。

随机网络 ER模型

定义： 随机图是一个有N个节点，每对节点以p概率相连的图。

平均度<k>= p*(N-1)

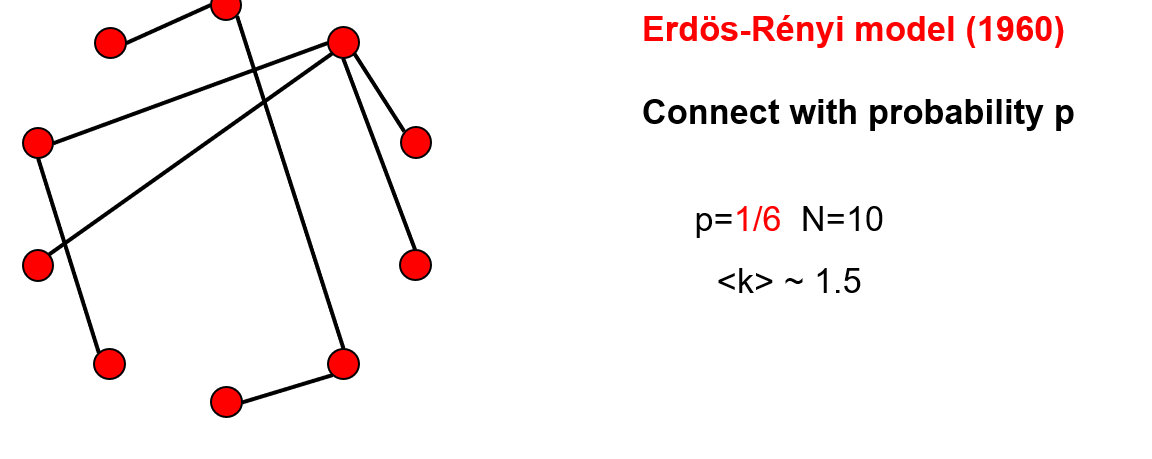
上图左边的图是随即图进行一次采样的结果，是随机生成的一种结果。

定义：有 N 个节点，任意一对节点以概率 p 相连。

这句话对应的就是 G(N,p)模型，也是现在最常用、最直观的定义。

G(N,L)模型与上面的不同，这个的意思是，有N个带编号的节点，随机放L条边，所有恰好有L条边的图等概率，平均度=2L/N。

随机网络与二项分布

在G(N, p)模型中，边数L的概率分布服从二项分布。

P(L):G(N,p)下的图，边数为L的概率

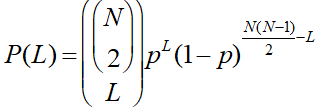
C(N, 2)意味着最大的边数（也就是全部连接起来）。

C(C(N, 2), L)意味着从所有的边里面选L条边存在，后面就是标准的二项分布了，p意味着边存在的概率，上面是边数，后面就是不存在的边数。

均值=Np,方差Np(1-p)。

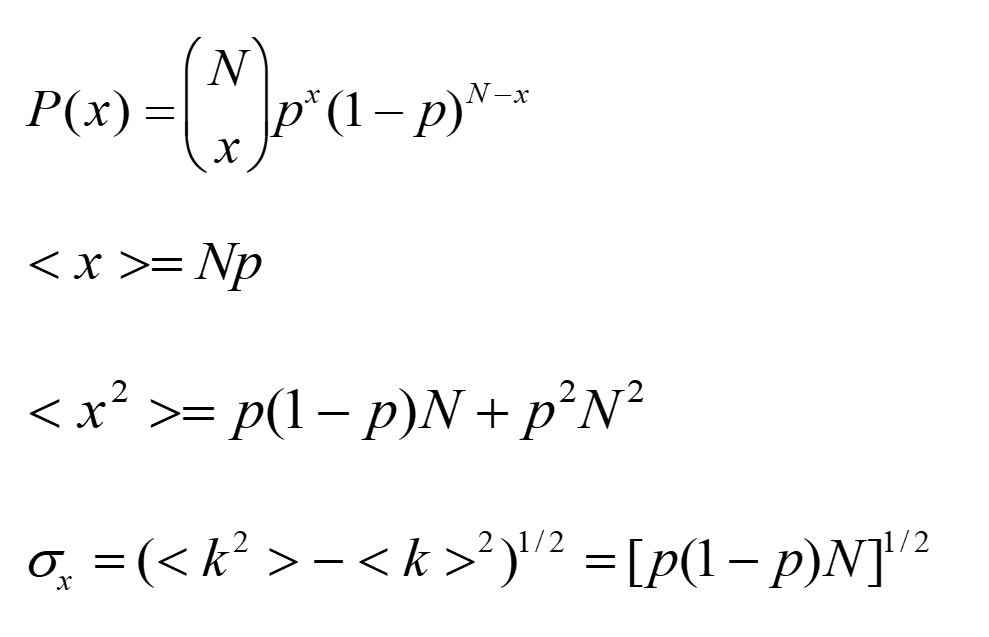
网络演化

即随机网络中的相变现象。<k>比较小的时候，是一个碎片化的网络，随着连接概率增大，会出现一个相变，在<k>=1附近。

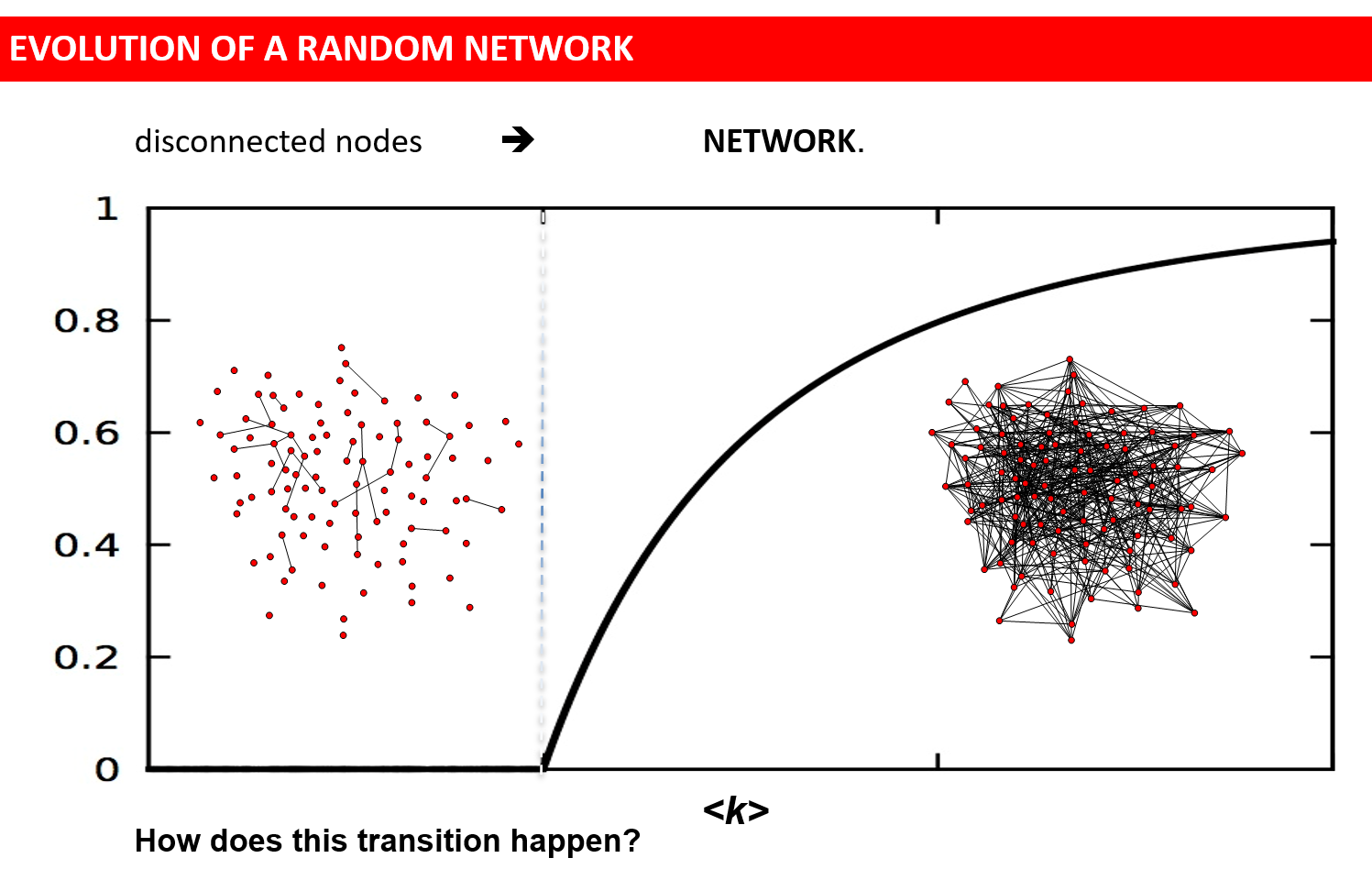
这张图展示的是：
当随机网络的平均度 ⟨k⟩ 增大时，
网络从“大量孤立小簇”突然跃迁为“一个巨型连通分量（Giant Component）”的过程。

随机网络的度分布

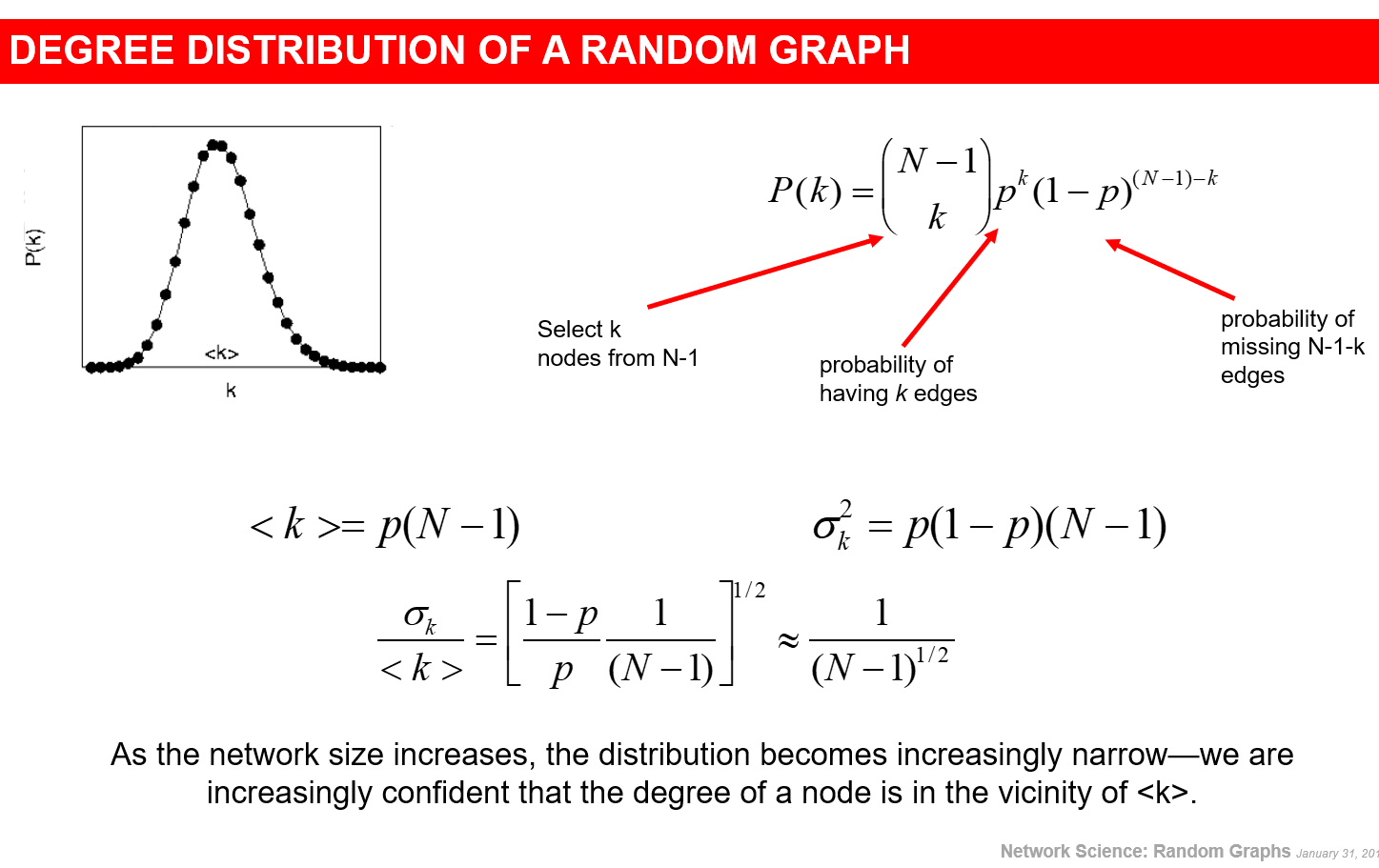
相当于是，固定一个节点，从其他N-1个节点里面选k个节点与这个节点相连（意味着度为k）。

对于大N小k，引入泊松分布来进行近似。

第四节课

重点：无标度网络的相关基本概念（比如Hub现象）。后面要知道几个生成模型（Generating networks with a pre-defined p_k）。

无标度网络

大部分的节点度都很小，小部分度非常大(这类节点称为Hub)，不管把网络放大还是缩小，这种分布形态都不会变（尺度不变性）。

和随机网络对比，无标度网络符合幂律分布，随机网络属于是泊松分布。

配置模型

重点：如何把自环，重边除去（课上讲过）。

Configuration model 是：在“给定度序列”的前提下，随机连接边，生成“最大随机性”的网络模型。

自环和重边：当N区域无穷的时候且度不太极端的情况下，自环和重边的概率区域0.

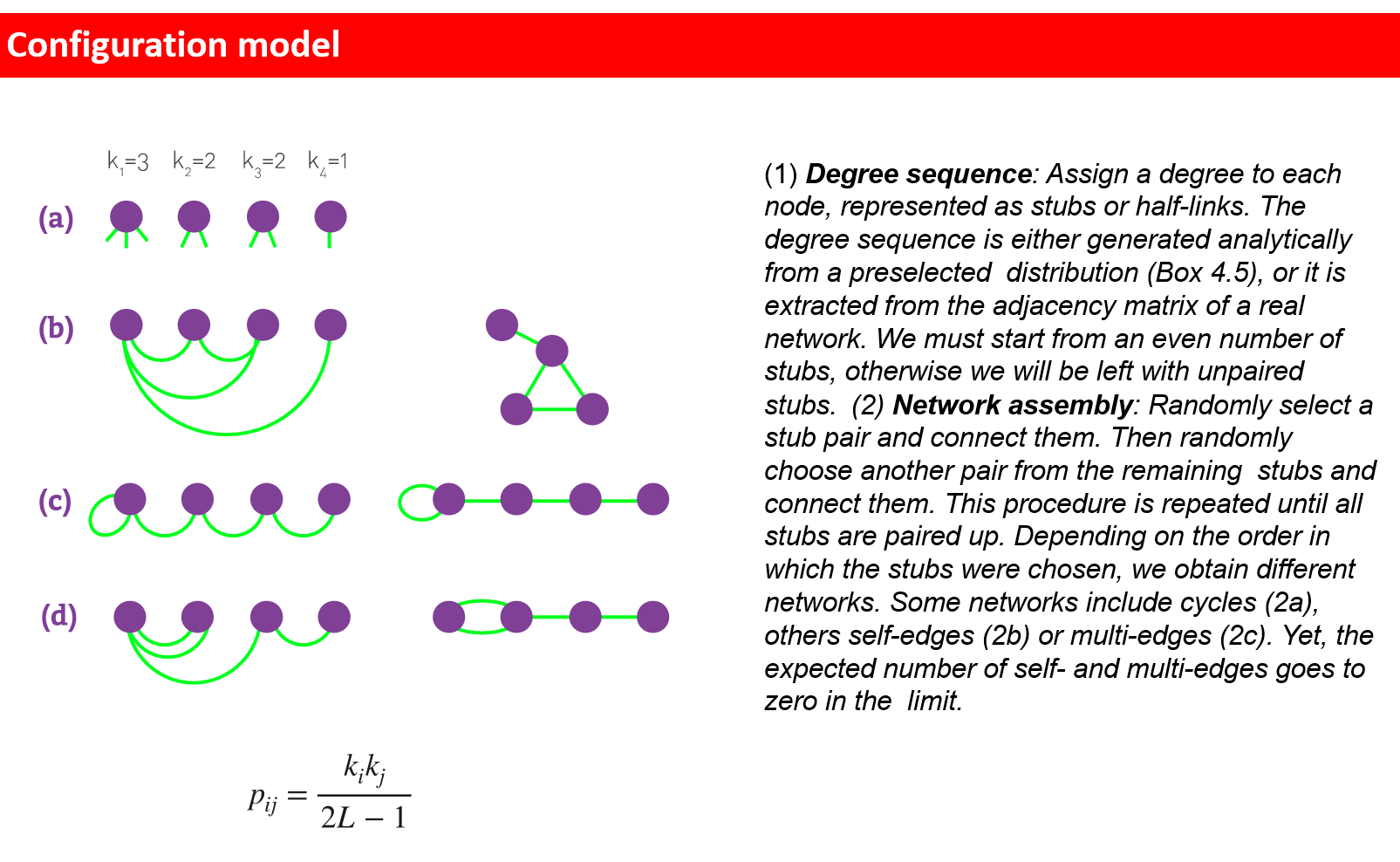
自环和多边

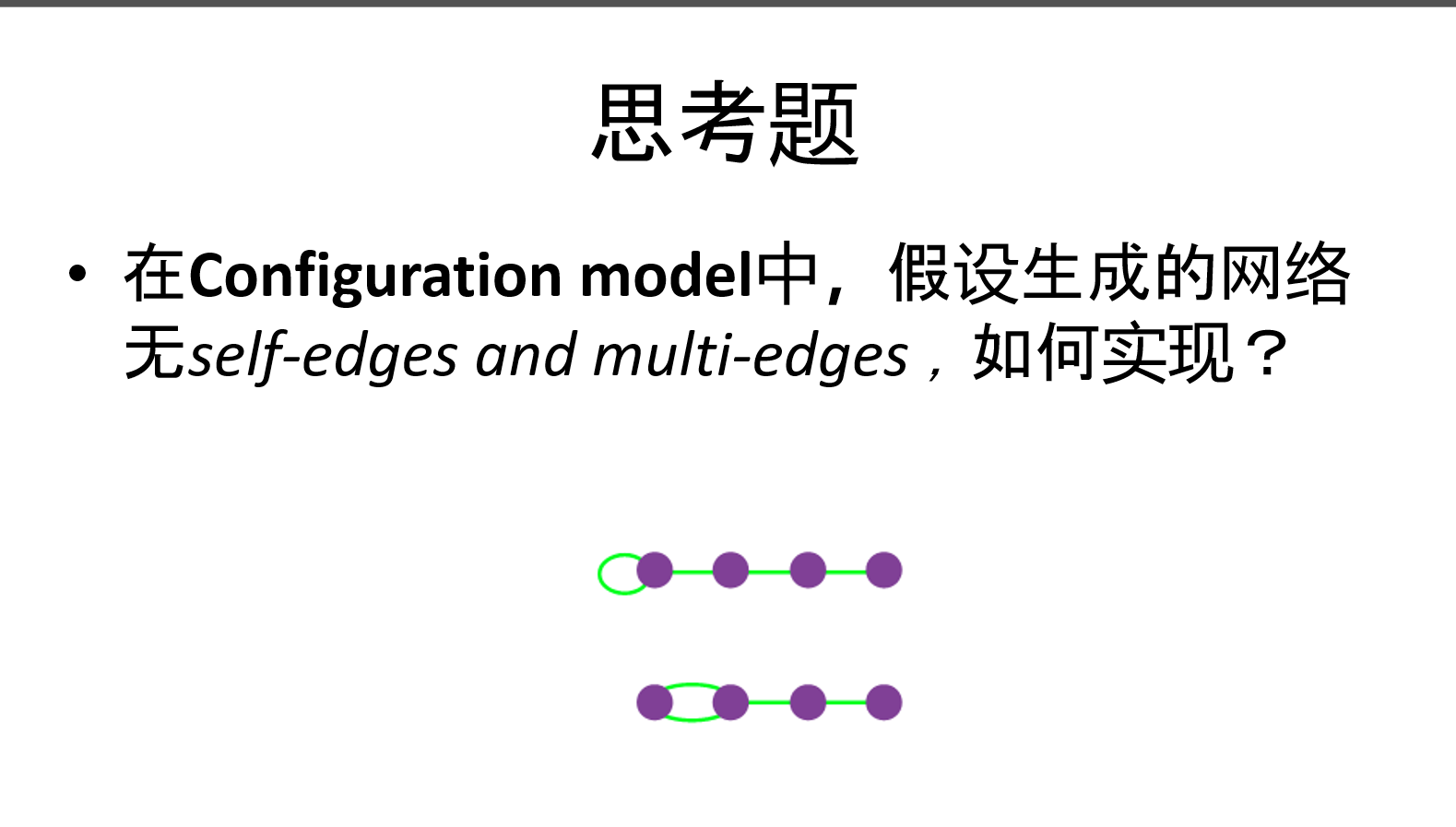
如何去除？

老师课上讲的方法：

如果有自环节点 u（显然它的度为2），我们需要找一对节点a,b，他们互相连接，度都为1，这时，我们去掉u的自环边，去掉a,b相连的边，重新连接，变成a--u--b，这时，a,u,b他们的度都不变，而且自环得以除去。

如果有多边节点a==b，我们同样还是找一对互相连接的节点c和d（c--d），去掉a和b重边的一条，去掉c和d的边，重新连接形成c--a--b--d即可。

第五节课

重点：描述一下BA网络的生成过程。

BA网络的生成

两步骤：Growth（成长） + Preferential Attachment（优先连接）

Growth（成长） + Preferential Attachment（优先连接）

BA 模型由两个基本机制构成：网络的生长（growth）和优先连接（preferential attachment）。在每个时间步，一个新节点加入网络，并以与节点度成正比的概率连接到已有节点。

链路选择模型

Link Selection Model

Link selection model 中，新节点不是直接选择节点，而是随机选择一条已有的边，并连接到该边的一个端点。由于度为 k 的节点连接着 k 条边，该机制自然导致连接概率与节点度成正比，从而产生线性优先连接。

Copying Model （描述）

第六节课

BA模型与BB模型

BA模型不是错的，而是不够丰富，比如BA模型中，γ=3，但是现实世界里面γ是一个范围。BA网络中，平均聚类系数C(N)~1/N，而现实世界中，平均聚类系数不随网络变大而消失。BA模型中只做了两个基本假设，也就是线性增长（导致平均度是常数，不和N有关）和线性优先连接（导致幂律）。

BB模型在BA模型上，在优先连接中引入了“节点适应度”，让节点竞争连接资源。

Fitness Model

总结：Fitness Model是对BA Model的扩展，引出 Fitness Model：通过给节点引入“内在适应度”，解释为什么现实网络中，后来但更优秀的节点也能成为超级 Hub。（注意FitnessModel === BBModel）

第七次课（A）

“一个节点更倾向于和‘度数相似’的节点相连，还是相反？”

这是从“有没有 Hub（度分布）”进一步走向
👉 “Hub 彼此怎么连” 的问题。

三种形式的网络

1️⃣ Assortative（同配网络 / 正相关）

定义：

高度节点倾向于和高度节点相连
低度节点倾向于和低度节点相连

图中现象：

• 红色 Hub 之间大量互连

• 形成“核心圈子”

常见于：

• 社交网络

• 合作网络

• 学术合著网络

📌 直觉：

“大佬只和大佬玩”

2️⃣ Neutral（无相关 / 随机）

定义：

节点连接不依赖度
符合随机期望

图中现象：

• Hub 之间既不特别连

• 也不刻意回避

典型模型：

• E-R 随机图

• 标准 BA 模型（近似）

3️⃣ Disassortative（异配网络 / 负相关）

定义：

高度节点倾向于和低度节点相连
Hub 之间反而避免相连

图中现象：

• Hub 像“中心服务器”

• 周围连着大量小节点

• Hub–Hub 边很少

常见于：

• 互联网（AS 级）

• 生物网络

• 技术网络

📌 直觉：

“中心节点负责服务边缘节点”

如何刻画网络的同配型

神秘的图（e_jk矩阵）

平均最近邻度

平均最近邻度（Average nearest-neighbor degree）

怎么看同配还是异配

看图，大概是常数就是中性，正相关同，负相关异

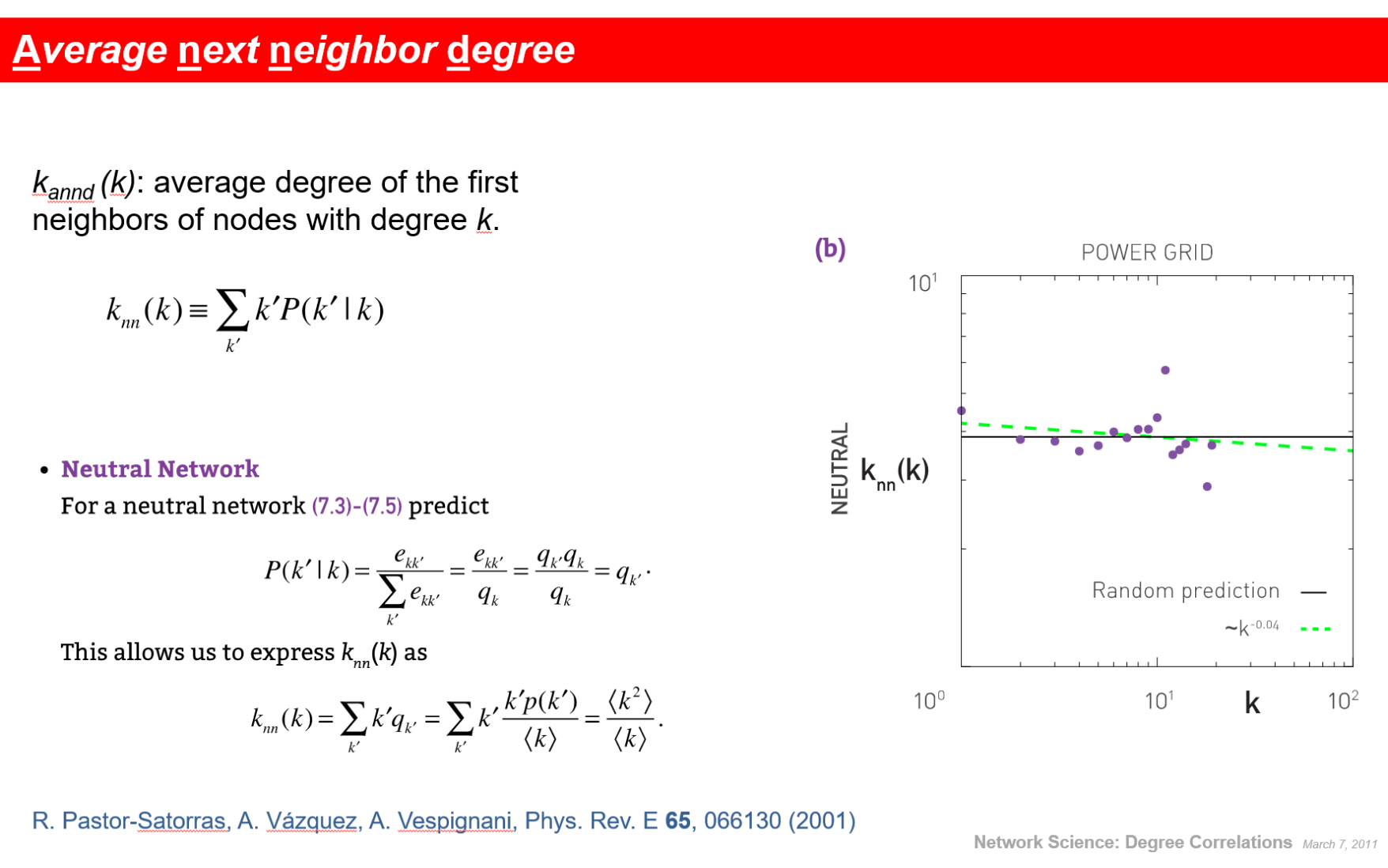
度相关系数

如果是中性网络，r近似等于0而不是精确等于0.

改变同配性

“我们可以通过置换的方法改变网络的同配性，有些网络能改变，有些改变不了”

第七次课（B）

加权网络是什么，怎么定义。

网络中的边不仅表示“是否相连”，还携带一个数值权重，用来表示连接的强弱、容量、频率或重要性。

肥尾分布（fat-tailed）

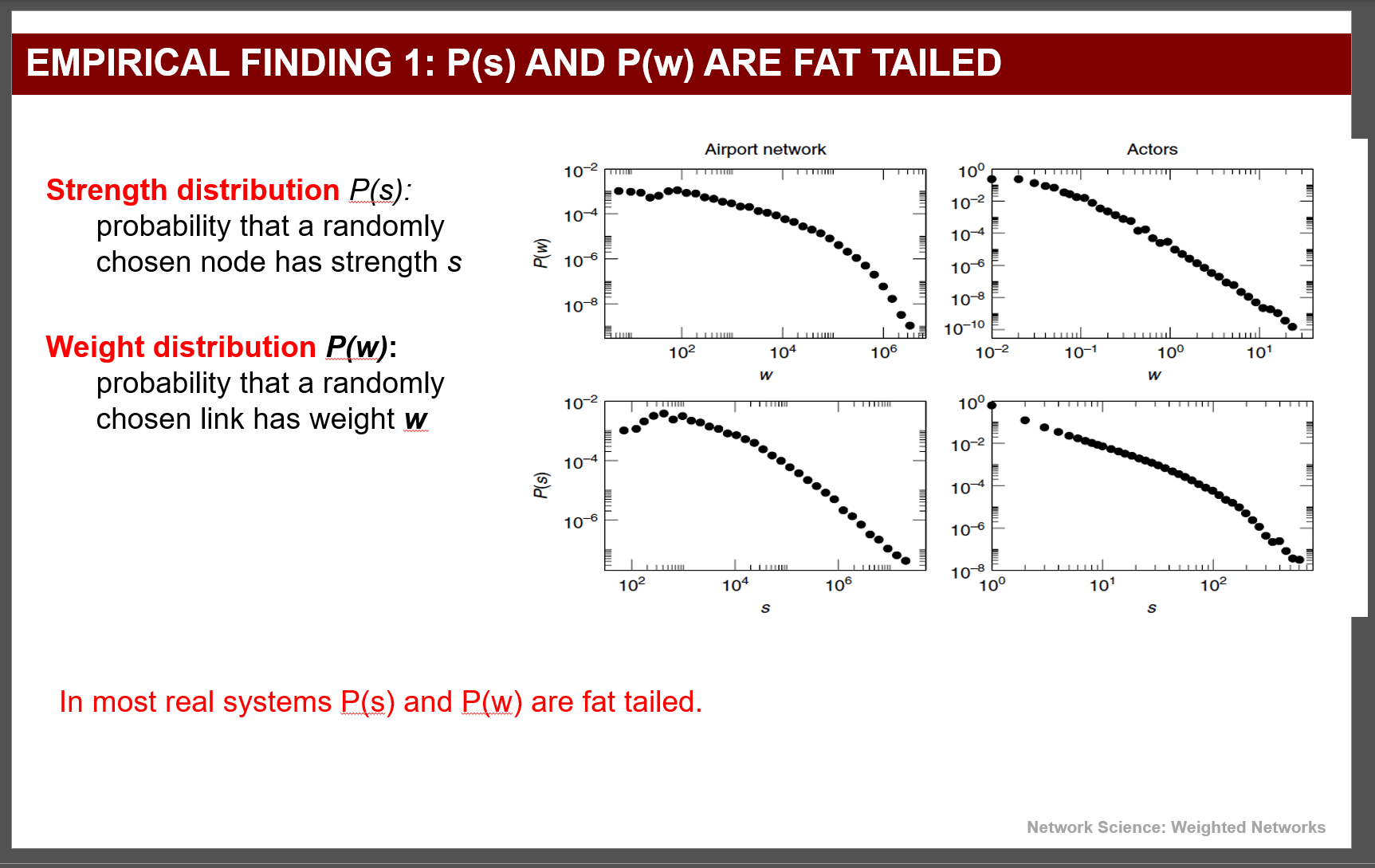
注：加权网络的（度）相关系数不考。

第八次课（重点）

社团（社区）检测

社团的概念

社团是指网络中一组节点，其内部连接显著强于外部连接，从而在结构或动力学意义上形成相对独立的子结构。

两假设：

i) 一个社团对应一个连通子图。

ii) 社团对应网络中的局部高密度区域。

社团不是“连在一起的一堆节点”，而是“连得特别紧的一堆节点”。

社团检测的方法

Kernighan–Lin（KL）算法。

层次聚类思想

如果我们能定义“两个节点有多相似”，能不能只靠相似性，把网络一步步聚成社团？

层次聚类的两大策略：Agglomerative（凝聚型，自底向上），Divisive（分裂型，自顶向下）

对于相似度：

两大策略：

至少要会其中一种方法！

社团检测的应用

模块度

评价社团划分的好坏

模块度（Modularity，记作 Q）是衡量一个网络划分成“社团”有多好的经典指标，也是社团检测中最核心、最常考的概念之一。

随机网络没有社团结构

重叠社团（Overlapping）

要知道概念。

第九次课

网络鲁棒性

怎么评价网络的鲁棒性

第十次课

传染病模型

例子 非典型肺炎例子、COVID-19例子。

传染病模型有哪些

其他类型题目

自由发挥题目：作报告相关的问题，给你一个类似的场景描述一下存在某些网络现象？网络中存在什么问题？

回答四段式：

考后感

大部分题目与上述的重点完全一致

算Kannd，算整个图的最短路径（考试卷子给了一个12个节点17个边的图，让我们写每对节点的最短路径，并且计算平均最短路径和最短路径的分布）。。。

然后就是要对比BA网络、CopyingModel/Link SelectionModel、和配置模型在实际生活中的用途，他们的区别。

重点其实就是和课程名字一样，复杂网络的“基础”和“应用”，重点在应用上，你要会表述，会写小作文。

还有个比较难的知识点我没复习到的，就是对于无标度网络的鲁棒性的计算，N'/N具体怎么算，对于网络的随机攻击或者是对网络进行针对性攻击下的区别。