关于

主讲教师：Patrick Rebeschini

复杂类相关证明

关联

NTIME 与 NSPACE

NTIME(t(n)):

所有能被某台NTM在时间O(t(n))内判定的语言的集合。

NSPACE(s(n)):

所有能被某台NTM在空间O(s(n))内判定的语言的集合。

General

P ⊆ NP ⊆ PSPACE ⊆ EXPTIME

P ⊆ coNP ⊆ PSPACE

NP ⊆ EXP

P ⊊ EXPTIME

PSPACE ⊊ EXPTIME

NL = coNL (Immerman-Szelepcsényi Theorem)

P = coP

P ?= NP

NP ?= coNP

P ?= PSPACE

NP ?= PSPACE

重点说明

四大复杂类（P，NP，(N)PSPACE，(co)NL）判断他们之间的关系，并说出原因。

P⊆NP:

For any L ∈ P, we can construct a NP verifier, certification w can be empty or ignore, verifier V(x, w) runs the P's algorithm A(x), accepts iff A(x), else reject.

(Deterministic machines are special case of Nondeterministic machines.)

L⊆NL:

Same as P and NP.

(Deterministic machines are special case of Nondeterministic machines.)

NP ⊆ PSPACE:

思路：NP由NTM决定，NTM是多项式时间，所以NTM只能在NTIME内访问NSPACE，由Savitch定理可以把NSPACE转换成DSPACE，就可以说明NP属于PSPACE。

For any L ∈ NP, There's a nondeterministic Turing Machine M that for any input w(length is n), M can define L in poly time p(n).

Since machine M can run at most p(n) steps, it can visit at most O(p(n)) tape cells, Therefore it uses polynomial space. In particular, NTIME(p(n)) ⊆ NSPACE(p(n)). Hence, L ∈ NSPACE(p(n)).

By Savitch's Theorem, for any s(n) >= logn, NSPACE(s(n)) ⊆ DSPACE(s(n)^2).

Let s(n) = p(n), L ∈ DSPACE(p(n)^2).

Because p(n) is polynomial, p(n)^2 is also polynomial.

So, DSPACE(p(n)^2) ⊆ PSPACE, L ∈ PSPACE.

So, NP ⊆ PSPACE.

NL ⊆ P:

For language L ∈ NL, for any input w(length is n),NL machine at most uses O(logn) bits.

O(logn) bits can represent 2^(O(logn)) = n^(O(1)) situations, So we can use BFS to visit all situations, this problem is in P.

so NL ⊆ P.

NL = coNL:

Immerman-Szelepcsényi theorem.

PSPACE = NPSPACE:

Savitch Theorem.

首先 PSPACE ⊆ NPSPACE 显然成立

然后，我们引入Savitch定理：

NSPACE(s(n)) <= DSPACE(s(n)^2) , s(n) >= logn，

由于我们讨论的是Poly下的，所以取s(n) = n^k

所以NSPACE(n^k) <= DSPACE(n^2k)

DSPACE(n^2k) ⊆ PSPACE

所以 NPSPACE ⊆ PSPACE

综上, NPSPACE = PSPACE.

规约

多项式时间规约

对数空间规约

L

证明在LogSpace内，我们只需要写一个算法，让其只占用最多LogSpace空间即可。

比如这一题，我们使用一个计数器，初始化为0，然后此时从最左边开始读取，遇到左括号就+1，遇到右括号就-1，注意，如果当前数值为0且遇到了右括号，就reject。然后等读取到最后一个括号并且对数值进行操作后，如果数值不是0，就reject。如果数值是0，就accept。

这个算法只用到了当前括号索引和一个计数器，都是数字，数字（二进制或者十进制）都是Log_2(xxxx)或者Log_10(xxxx)，即都是LogSpace的，所以A是L。

NL & coNL

证明NL的时候，如果觉得复杂，就把它取反，证明某个问题是coNL，然后由Immerman-Szelepcsenyi定理，coNL=NL，即可得到其是NL。

NL问题的证明，作业题中如二分图问题就是NL问题，详见”二分图是NL“。

NL-COMPLETE

NLC的证明与NPC证明一样，只要说明一个语言L是属于NL的，且是NL-Hard，他就是NLC。

同样我们需要选择一个NL-Hard的问题来归约到它，才能证明它也是NL-Hard。

常用来规约的NL-Hard问题有PATH（也叫ST-CONN）。

PATH = {<G, s, t>| 图G中，s 和 t 之间有有向/无向的路径}.

2-SAT（子句有两个literal的布尔可解性问题，可以由PATH规约来）

规约方案：

对PATH来说，对每个点抽象成x_u布尔变量，如果是真就是可达，如果是假就是不可达。

然后，对于每个边，加入蕴含，比如u->v有边，就加入x_u -> x_v蕴含式(也就是非x_u 析取 x_v)，符合2SAT。

同时，加入两个单一字句（x_s和非x_t），代表x_s是初始节点，x_t是最终节点，初始节点肯定可达，最终节点在没有路径的情况下不可达。

这样，PATH问题就变成了2-SAT的问题。同时2SAT也可以来证明有向图。

证明其是NL-Hard：

使用Path来规约，Path = {<G, s, t> | 图G中有s到t的有向路径}。

我们通过构造一个新图G'，使得G'中存在原来的V和E，然后遍历所有节点（保存curr节点的index，s和t节点的index），加入新边：所有节点->s，t->所有节点，这样即保留了s和t之间原来的路径，又加了t到s的路径，并且由于保存的都是index，所以是Logspace下的规约，所以PATH <=(L) STRONG-CONNECTED，STRONG-CONNECTED是NL-Hard。

下来证明其是NL：

考虑其补问题coSTRONG-CONNECTED = {<G, u, v> | u节点与v节点没有有向路径}。

我们依旧使用NL的算法，保存curr_index, u_index, v_index，然后对图进行遍历，空间依旧是LogSpace，所以co-STRONG-CONNECTED是NL，由Immerman-Szelepcsenyi定理得 coNL = NL，所以STRONG-CONNECTED 是 NL。

所以， STRONG-CONNECTED 是 NL-Complete。

P

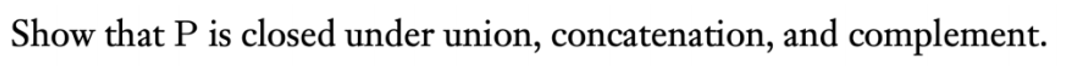
如果P是P class

对Union，设A,B∈P，则存在多项式时间内算法Ma(x)，Mb(x)，分别决定A和B

A∪B意思就是输入x，Ma和Mb中，只要有一个接受就接受。

时间复杂度是两个相加，也是多项式。

对Concatenation：

前面一样，但是输入是w,对w进行切分，从首位到末位，只要有一个输入能分别让Ma,Mb接受，就接受

时间复杂度，由于要切分n+1次，所以是(n+1)poly(n)，依旧是多项式时间

对Complement：

将结果翻转。

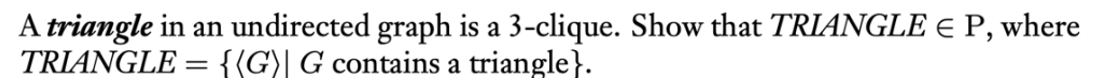
这一题要证明TRIANGLE∈P，只需要给出一个算法，让其在多项式时间内能解决即可。

这类题比较简单，比如这题就是可以给出，遍历图G，<a,b,c>为3个不同的节点，只要检测<a,b>,<a,c>,<b,c>之间是否存在边，即可说明G contains a triangle，对于遍历则是O(n)*O(n)*O(n) = O(n^3)，属于多项式时间。所以TRIANGLE ∈ P。

NP

定义+扩展

图同构的证明。我们需要给出证书，和这个证书如何在多项式内验证的验证器。

图同构的意思是，存在一个双射（bijective）函数Π: V(G) -> V(H)，使得：

任取u, v ∈ V(G), (u, v) ∈ E(G) <-> (Π(u), Π(v)) ∈ E(H).

证书就是Π函数。

我们只需要对于每个G中的边(u, v)，计算(Π(u), Π(v)) ∈ E(H)是否成立即可。

所以时间复杂度在多项式时间内，所以ISO∈NP。

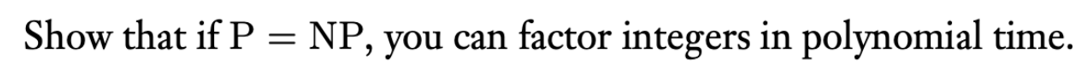
由于分解整数需要给出一个具体的答案，但是P和NP问题解决的都是可行/不可行这类的问题，所以我们需要构建一个问题。

HAVE-FACTOR = {<a, b, c> | a=yz，其中一个因子 b <= y <= c }，证明这个问题是NP，因为我们可以给出一组a,b,c，我们只需要对所有b~c的整数遍历一遍，就可以确定a的一个因子y在[b,c]。由于P=NP，所以这个问题实际上可以在多项式内解决。对于任意一个整数，我们对其进行因子猜测，令a = 这个整数，b = 2，c = 这个整数，使用算法在Polytime解决HAVE-FACTOR问题，然后进行二分查找，由于二分查找也是多项式时间内，所以整个算法都是多项式时间的，最终我们就可以精确的找出y的值，然后对y进行递归的分解，由于对于一个整数n，它最坏的情况就是2的幂，也就是说，它最多有log_2(n)个因子，所以递归分解次数肯定是多项式内的，不断进行递归直到这个整数被完全分解，还是多项式时间。

coNP

定义+扩展

首先不能说明MIN-FORMULA是NP，所以根据题意就是属于P，因为MIN-FORMULA不一定属于NP。

正确做法是取其反。

MIN-FORMULA = {<φ> | 任取一个φ'与φ等价，φ'长度都不会少于φ}。

NOT-MIN-FORMULA = {<φ> |存在一个比 φ 更短的布尔表达式φ'，且φ与φ‘在逻辑上等价}。

由于我们可以给出一个certification，可以在多项式时间内验证φ‘是否比φ短，多以NOT-MIN-FORMULA显然是NP。

所以MIN-FORMULA∈coNP，然后用上题目的条件 P = NP，由于coNP = coP = P，所以coNP = P。

所以MIN-FORMULA ∈ P。

第二问在PSPACE。

NP-COMPLETE

NPC问题是NP里最难的一类的判定问题。

证明L是NPC问题，我们需要先证明L是NP问题。

然后证明L是NP-Hard问题（即所有NP问题都可以多项式时间内规约到它）。

证明L是NP-Hard问题可以使用多项式规约的传递性，我们选择一个已知的NP-Hard问题，在多项式时间内归约到L，就可以证明L不比这个问题简单，就可以说明L是NP-Hard。

L∈NP + L∈NP-Hard --> L ∈ NPC.

常见用于规约的NPC问题有：

SAT 布尔公式φ可满足性。

哈密顿路径问题（一个路径，遍历了每一个点）。

a. 用BFS遍历，BFS只用多项式时间就可以得到最短路径，看是否是小于等于k即可，所以SPATH ∈ P.

b.

先证明LPATH是NP：

给定一组从a到b的简单路径，我们可以在多项式时间内验证其是否至少是k，所以LPATH是NP。

再证明LPATH是NP-Hard：

由UHAMPATH规约，UHAMPTH = {<G, a, b>| 无向图G中从a到b有一条哈密顿路径}。

令UHAMPTH中的G有m个节点，我们令新图G‘=G，k=m-1，由于原图中a到b有一条哈密顿路径，长度肯定是m-1，因为只有m个节点。

所以新图中，a到b的路径最短至少就是m-1。而且我们规约只是设置了k，必然在多项式时间内完成。

所以UHAMPATH <=p LPATH。

所以LPATH 是 NP-Complete.

a. !=-asignment就是3CNF里面的literal，true和false至少一个，所以它的取反依旧是true和false至少一个，所以还是!=-assignment.

b. 3SAT就是3CNF的可满足问题，其中每个字句都是true，但是字句内的文字没有至少一个true一个false的要求，所以我们需要在这里进行多项式时间内的规约，让他每个字句都有一真一假。我们令3SAT中的每个字句拆为两部分，第一部分就是前面两个变量加上一个新变量Zi，第二部分是~Zi与最后一个变量，再加上一个新变量b，这样当SAT满足时，每个字句满足，也就是yi里面至少一个真，假如第一个或者第二个是true，zi可以为false，使第二个字句成立的同时，第一个字句中满足3CNF，如果y3也是真，b可以设置为假来满足3CNF，如果y1 y2全是假，zi设置为真，如果y3也是假，设置b为真即可。对于每组字句都进行这样的字句扩充，时间复杂度是多项式时间内的，完成了多项式时间规约。

所以 3SAT <=p !=SAT。

c. 由于可以给定一组certification，我们可以在多项式时间内计算!=SAT的3CNF取值是否为真，所以!=SAT是NP问题。

由于3SAT是NP-Complete问题，且!=SAT可以由其规约而来，所以!=SAT是NP-Hard问题。

综上所述，!=SAT 是NP

PSPACE

定义+扩展

要证明PSPACE-Hard问题都是NP-Hard问题，要用到：NP 包含于 PSPACE 这个基本定理。

取语言 A ∈ PSPACE-Hard，意味着 任意L∈PSPACE，都能在多项式时间内规约到A。

任意取L' ∈ NP，由于NP 包含于 PSPACE，L‘∈PSPACE，所以L’可以在多项式时间内归约到A。

所以A也是NP-Hard。

重点：使用SAT当作桥梁，用规约来反向推。

由于SAT是NP-Complete，所以SAT是NP-Hard。

由题可知，SAT是PSPACE-Hard。

由于PSPACE包含NP，所以SAT是PSPACE-Complete。

由于SAT是PSPACE-Complete，所以任意L∈PSPACE，都可以多项式时间归约到SAT。

由于SAT是NP，所以L是NP。

所以，PSPACE 包含于 NP，又 NP 包含于 PSPACE，所以PSPACE = NP。

第一问在coNP。

解决第二问：

要证明MIN-FORMULA是PSPACE，我们需要给出一个在多项式空间内能验证MIN-FORMULA的算法。

第二问就没有假设P=NP了。

MIN-FORMULA = {<φ> | 任意φ' === φ， |φ‘| >= |φ|}。

我们只需要对n < |φ|的布尔公式进行枚举检查：

首先枚举所有长度小于|φ|的布尔公式进行枚举，

对于每个布尔公式，检查它们是否与φ的变量相同，并且检查它们是否等价。

如果等价，就说明找到一个比φ更短的formula，返回reject。

如果对于所有的布尔公式都没有找到一个比φ更短的，返回accept。

空间占用：只占用保存当前布尔公式的空间，这部分空间是O(n)，测试等价时保存所有变量的取值{0, 1}，一个长为n的布尔公式最多有n个变元，所以空间占用最多为O(n)，所以MIN-FORMULA∈PSPACE。

博弈类问题，证明是PSPACE也是一样的，需要你编写一个算法，使用这个算法来证明原问题是能在多项式空间内被解决的即可。

GM的意思是，从当前局面开始，对“X”有一个必胜的策略，也就是无论“O”怎么走，“X”只要按照必胜策略，就能赢。

考虑以下算法：

i) 从局面B开始，

ii) 假如轮到X下棋，且X这一步就能赢，返回true，

iii) 假如轮到O下棋，且O这一步就能赢，返回false，

iv) 假如轮到X下棋，但是这一步不能赢，则需要在子局面进行递归：

对于n*n的棋盘，每个位置都下一遍，递归调用该算法，并且设置初始子局面是下的某个位置。

对于所有的返回值，如果只要有一个是true，就返回true。

v) 假如到O下棋，但是这一步不能赢，则需要在子局面进行递归：

对于n*n的棋盘，每个位置都下一遍，递归调用该算法，并且设置初始子局面是下的某个位置。

对于所有的返回值，必须所有的局面是true，才能返回true（因为这是O下的，但是我们题目要求O不能决定胜负，因为从这个B局面开始X是必胜的）。

对于结果，算法结果是true则返回accept，算法结果如果是false，则返回reject。

空间分析：由于是递归，每次递归需要保存n*n的棋盘，空间复杂度是O(n^2)，由于棋盘最大是n*n，所以递归深度最大也就是n^2，所以，空间复杂度是O(n^4)，依旧多项式。

所以 GM ∈ PSPACE。

SAT 的定义以及证明应用

SAT问题的定义，逻辑公式的可满足性（如何判断）

怎么去证明SAT的问题，思路是什么

SAT是NPC问题（Cook-Levin定理）

定义

SAT = {<φ>| φ is satisfiable boolean formula}。

重点

复习作业题里面SAT证明的应用

先证明DOUBLE-SAT是NP：

因为给定一组certification，可以在poly-time内去验证这个问题，所以它是NP类问题。

下来证明DOUBLE-SAT是NP-Hard：

将SAT多项式时间归约到DOUBLE-SAT，SAT = {<φ> | φ是可满足的布尔表达式}，DOUBLE-SAT={<w>|w = φ AND (x or NOT x)}，由于加入一个变元是在多项式时间内的，且加入一个变元后，该布尔公式有至少两个满足赋值（x=0或者x=1），φ本来就可满足。所以SAT <=p DOUBLE-SAT，DOUBLE-SAT是NP-Hard。

所以DOUBLE-SAT是NP-Complete。

CNF 的子句求值解析

字句(clause)是若干文字(literal)的OR。

C=(ℓ1​∨ℓ2​∨⋯∨ℓk​)，求值规则：只要有一个文字为真，子句就是真。

CNF是若干字句的AND：

F=C1​∧C2​∧⋯∧Cm​，求职规则：必须所有子句都是真，CNF才是真。

图灵机模型

空间复杂度/时间复杂度的关联推导

多带图灵机的运行机制，如何分析图灵机的运行时间上限

定义

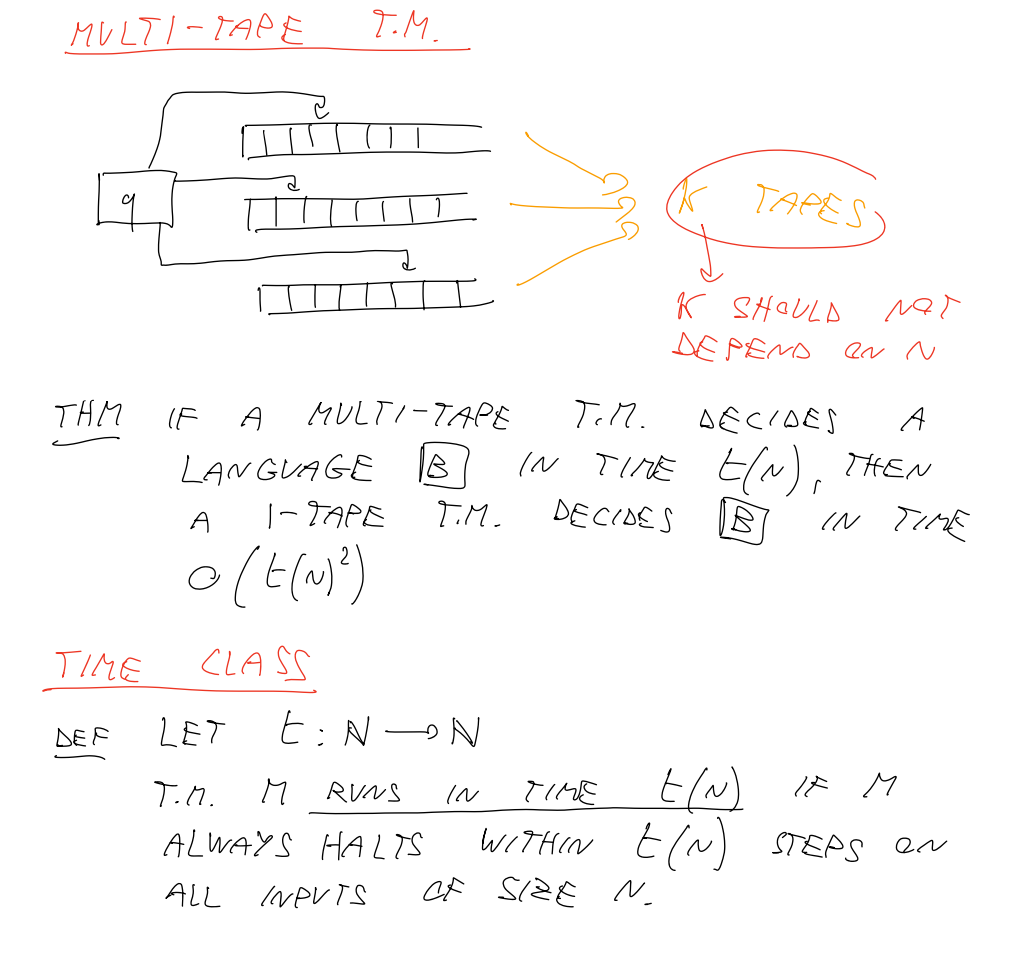
多带图灵机

时间与空间复杂度

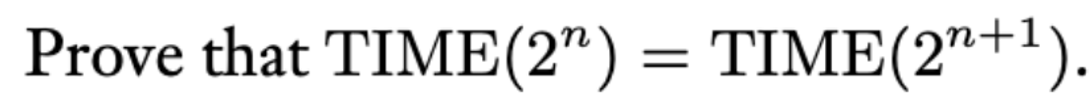
L ∈ TIME(f(n)) means: Exists a deterministic Turing Machine M and a constant c. For any length n inputs, M decides L in at most c*f(n) steps.

So, TIME(2^n) 包含于 TIME(2^(n+1)), 因为 2^n < 2^(n+1),L ∈ TIME(2^n),那么L也属于后面

We need to prove TIME(2^(n+1)) 包含于 TIME(2^n):

TIME(2^(n+1)) -> O(2^(n+1)), for any input length n, M decides L in at most c 2^(n+1) = (2c) 2^n. -> TIME(2^n)

So 后者包含于前者，所以相等

时间上界=>空间上界

DTIME(t(n)) ⊆ DSPACE(t(n)), NTIME(t(n)) ⊆ NSPACE(t(n)).

理由：在时间t(n)内，head最多遍历t(n)个cells，因为图灵机运行的规则是head可以在每一步右移/左移/不动，所以它使用的空间不会超过O(t(n)).

空间上界=>时间上界

DSPACE(s(n)) ⊆ DTIME( 2^s(n) )

NSPACE(s(n)) ⊆ DTIME( 2^s(n) )

理由：对空间为s(n)的机器，其配置数最多是2^(O(s(n)))，用确定性方法再其上进行BFS，最多就是指数时间。

N空间上界=>D空间上界

引入Savitch定理。

NSPACE(s(n))⊆DSPACE(s(n)^2)(s(n)≥logn)

这个定理可以直接推导出NPSPACE=PSPACE，也可以推出NP⊆PSPACE。

多带图灵机运行机制

1带模拟k带

若k带图灵机使用t(n)的时间，则1带图灵机可以在O(t(n)^2)内模拟。

理由：把k带的纸带交错编码在1带上，每模拟一步，需要扫描一遍编码区，并且找到各头位置并更新，扫描的长度是O(t)，重复t次就是O(t^2)。

无向图相关考察

二分图 定义+充要条件 2SAT?

二分图定义

二分图的充要条件

可 2-着色：能用两种颜色给所有顶点染色，使得每条边的两个端点颜色不同。

显然是成立的，因为二分图就是分成两个集合。

没有奇环：图中不存在长度为奇数的简单环（odd cycle）。

二分图=>没有奇环：

证明它的逆否命题，如果有奇环，那么对其相连的节点，从x1开始编号到xn+1,然后x1与xn+1相连，显然是奇数个环，这时候会出现问题，也就是如果划分集合，初始节点会即在L集合也在R集合，所以矛盾，所以不是二分图，于是原命题得证。

没有奇环=>二分图：

既然没有奇环，选择一个起点u，对于其距离为奇数的节点放入L集合，否则放入R集合，若存在一条边把两个同集合的节点连接起来，就会形成一个奇环，矛盾，所以原命题得证。

二分图问题是 NL

使用一个NL算法检测奇数环，如果是奇数环ACCEPT，然后由于coNL = NL，所以二分图就是NL问题。

二分图问题规约到2SAT

二分图的判定可以规约为2SAT问题。

对于每条边(u, v)，使用XOR进行2CNF编码：

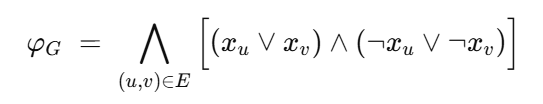
证明：

如果φG可满足，则图G是二分图。

对于一条边，采用φG来着色，对于其为真的边，着色为1，否则着色为0，由于x_u 析取 x_v，则u和v不可能是同假，由于非x_u析取非x_v，则u和v不可能是同真，所以u和v只能是两种不同的颜色，所以G是二分图。

如果G是二分图，则φG可满足。

如果图G二分，则其可以划分出两个集合L和R，其内节点分别着色为0和1.

显然对任意边(u, v)，u和v节点不能在上面的同一个集合中。

所以x_u 析取 x_v 为真，且非x_u析取非x_v为真，所以整个φG也就是真了。